Finite element method

Jul 12, 2022

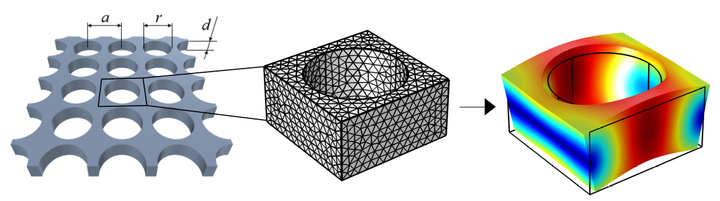
Finite element method ( FEM ) is a technique to solve differential equations for complex geometries, when analytical solution is not available. In the method, the system is divided into a number elements that form a mesh. Then solution of the equations can be found for the given system with certain boundary conditions.

FEM for obtaining phonon dispersion

An example above show the example of reducing an infinite phononic crystal structure into a unit cell with periodic boundary conditions, for which the elastodynamic equations are solved.

Solving the elastodynamic wave equation in the first Brillouin zone, we can obtain the phonon dispersion relation. From the dispersion, we can calculate various properties of the structure, including the group velocity, density of states, and the heat flux, as shown below.

Finite element method example

References